Discrete Event Simulation van teststraat modellen
Inleiding
De Toolkit inrichten testlocatie voor antigeentesten1 is een uitgebreid document om bedrijven te helpen met het opzetten van een (snel)testlocatie. Daar worden onder andere een aantal praktische modellen beschreven qua opzet en bemanning. In deze post een introductie hoe Discrete Event Simulatie2 kan helpen bij het inzicht krijgen en eventueel optimaliseren van een model.
Hieronder gebruik ik de naamgeving uit het hierboven genoemde document voor zover ze hier relevant zijn: inchecker, testafnemer en testverwerker.
We veronderstellen voor de rest van deze simulatie de volgende tijden in minuten.
inchecktijd <- 1
testafneemtijd <- 3
testverwerktijd <- 1
geopendtijd <- 8 * 60Hierbij gaan we er vanuit dat er 1 inchecker fulltime beschikbaar is en dat de checkin 1 minuut kost. Daarna gaat de client door naar de testafnemer en dat neemt ongeveer 3 minuten in beslag en daarna wordt de test verwerkt door de testverwerker. De client hoeft daarna niet te wachten op de uitslag, maar krijgt deze digitaal binnen 1 uur toegestuurd. De testlocatie is gedurende 8 uur open.
Voor de simulatie worden de simmer R packages3 gebruikt.
library(simmer)
library(simmer.plot)
library(simmer.bricks)
library(parallel)Simulatie teststraat model 2 variaties
Model 2 is bedoeld als een kleine teststraat met maximale bezetting. We veronderstellen het volgende m.b.t. hoe frequent er een nieuwe test client arriveert.
clientfrequentie_model2 <- 1/5 # 1 per 5 minutenOm een indruk te krijgen van de daarbij behorende distributie die in de simulaties hieronder gebruikt wordt een histogram:
qplot(rexp(1000, clientfrequentie_model2), geom = "histogram")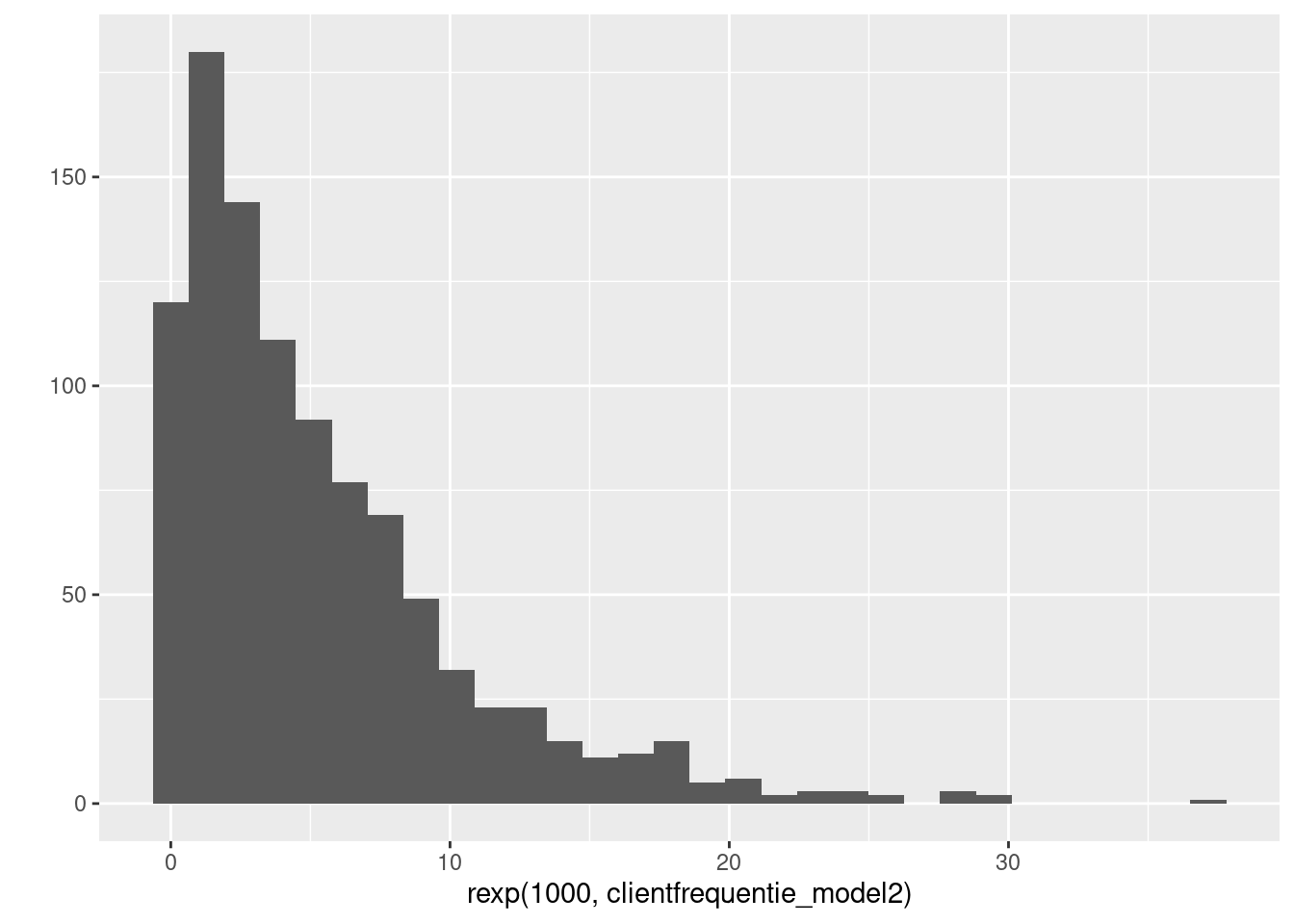
Model 2 basis teststraat
We starten met een basisversie van model 2, onderstaand de definitie van een teststraat traject voor een client.
set.seed(123)
teststraat_model2_traject <- trajectory("Teststraat model2 traject") %>%
visit(resource ="inchecker",
task = function() rexp(1, 1/inchecktijd)) %>%
visit(resource ="testafnemer",
task = function() rexp(1, 1/testafneemtijd)) %>%
visit(resource ="testverwerker",
task = function() rexp(1, 1)/testverwerktijd)Hieronder definieren een testlocatie simulator met 1 instantie van ieder van de eerder genoemde resources. Zoals gezegd komen de clienten volgens een bepaald random proces aan. We berpek het in eerste instantie tot 10 clienten.
testlocatie <- simmer("teststraatsimulator") %>%
add_resource("inchecker", 1) %>%
add_resource("testafnemer", 1) %>%
add_resource("testverwerker", 1) %>%
add_generator("ts_m2_a", teststraat_model2_traject,
function() {c(0, rexp(9, clientfrequentie_model2), -1)})Nu de definitie van de simulatie compleet is kunnen we deze uitvoeren, omdat er maar 10 clienten zijn zal de simulatie eerder stoppen dan de geconfigureerde 8 uren.
testlocatie %>%
run(until = geopendtijd ) %>%
now()## [1] 40.49252Na ongeveer 40 minuten uur hebben alle clienten het testtraject doorlopen. Hieronder nog een overzicht van de clienten gesorteerd naar aflopende wachttijd.
testlocatie %>%
get_mon_arrivals() %>%
transform(waiting_time =
round(end_time - start_time - activity_time, digits = 2)) %>%
dplyr::arrange(desc(waiting_time)) %>%
knitr::kable("html", digits = 2)| name | start_time | end_time | activity_time | finished | replication | waiting_time |
|---|---|---|---|---|---|---|
| ts_m2_a8 | 18.06 | 39.27 | 9.08 | TRUE | 1 | 12.13 |
| ts_m2_a6 | 15.77 | 29.34 | 3.22 | TRUE | 1 | 10.35 |
| ts_m2_a7 | 17.34 | 31.45 | 4.35 | TRUE | 1 | 9.76 |
| ts_m2_a5 | 14.18 | 29.08 | 8.14 | TRUE | 1 | 6.75 |
| ts_m2_a9 | 31.70 | 40.49 | 3.27 | TRUE | 1 | 5.53 |
| ts_m2_a4 | 13.90 | 23.99 | 9.66 | TRUE | 1 | 0.43 |
| ts_m2_a0 | 0.00 | 3.52 | 3.52 | TRUE | 1 | 0.00 |
| ts_m2_a1 | 4.22 | 5.82 | 1.60 | TRUE | 1 | 0.00 |
| ts_m2_a2 | 7.10 | 13.12 | 6.02 | TRUE | 1 | 0.00 |
| ts_m2_a3 | 13.75 | 17.83 | 4.09 | TRUE | 1 | 0.00 |
We kunnen ook naar het gemiddelde gebruik van de resources kijken, zegt nu niet zoveel vanwege het beperkte aantal clienten.
resources <- get_mon_resources(testlocatie)
plot(resources, metric = "utilization") +
ggtitle("Resource bezetting") +
ylab("bezetting")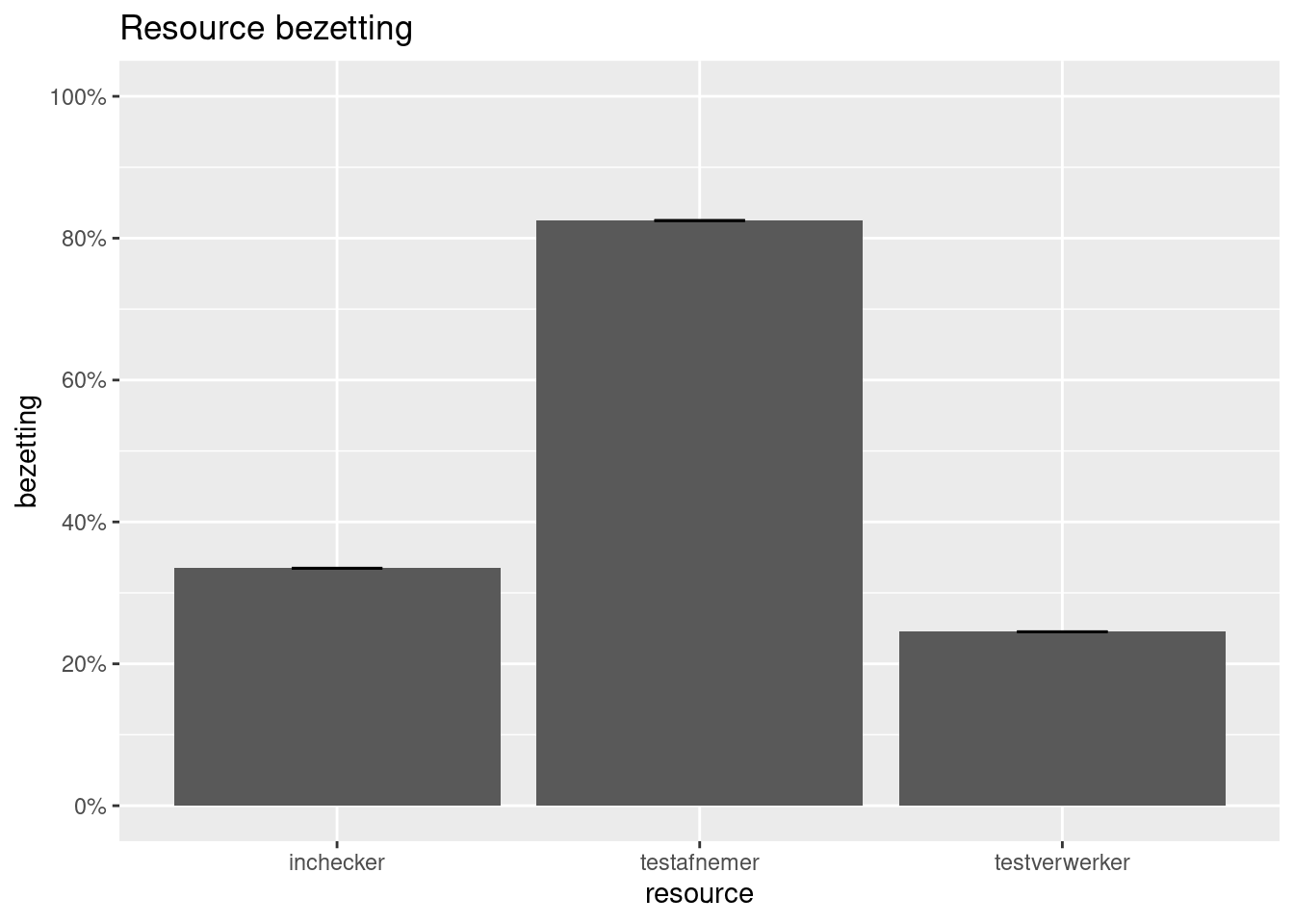
Verdeeld over de simulatietijd ziet het er als volgt uit.
plot(resources, metric = "usage", items = "server") +
labs(title="Resource gebruik gedurende de simulatie") +
xlab("tijd in minuten") +
ylab("in gebruik") 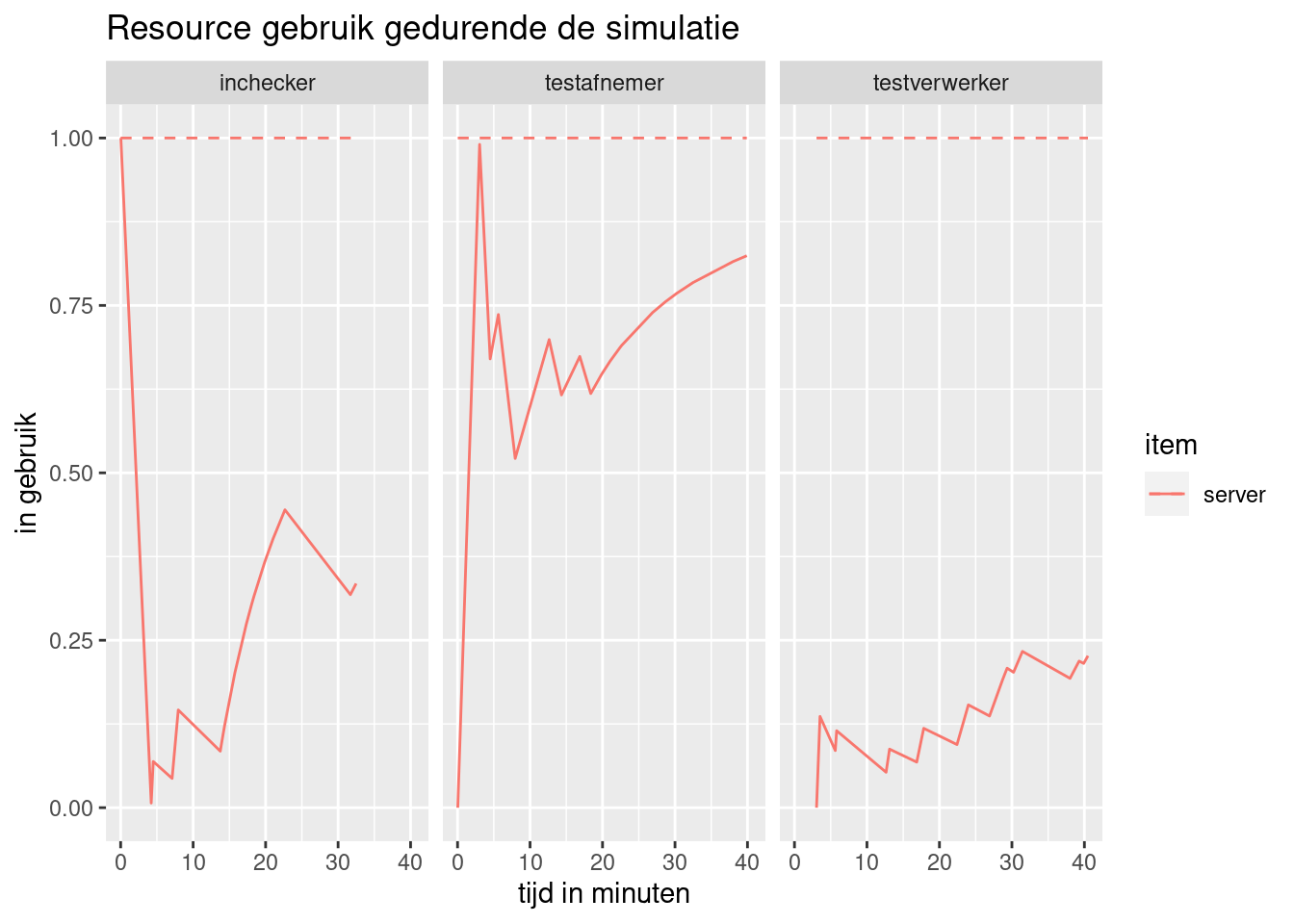
Model 2 teststraat met 2 testafnemers en gedeelde wachtrij
In deze variatie van de model 2 teststraat voegen we een extra testafnemer die wel de wachtrij deelt met de andere testafnemer. Het traject houden we hetzelfde als voor het basismodel en gaan weer uit van 10 clienten om diagrammen overzichtelijk te houden.
set.seed(123)
testlocatie_model2_2verwerkers <- simmer("teststraatsimulator2") %>%
add_resource("inchecker", 1) %>%
add_resource("testafnemer", 2) %>%
add_resource("testverwerker", 1) %>%
add_generator("ts_m2_b", teststraat_model2_traject,
function() {c(0, rexp(9, 1/clientfrequentie_model2), -1)})Nu de definitie van de simulatie weer compleet is kunnen we deze uitvoeren:
testlocatie_model2_2verwerkers %>%
run(until = geopendtijd ) %>%
now()## [1] 20.14837Verschillen zijn niet heel groot omdat het een beperkt
testlocatie_model2_2verwerkers %>%
get_mon_arrivals() %>%
transform(waiting_time =
round(end_time - start_time - activity_time, digits = 2)) %>%
dplyr::arrange(desc(waiting_time)) %>%
knitr::kable("html", digits = 2)| name | start_time | end_time | activity_time | finished | replication | waiting_time |
|---|---|---|---|---|---|---|
| ts_m2_b8 | 0.72 | 16.05 | 3.60 | TRUE | 1 | 11.72 |
| ts_m2_b9 | 1.27 | 20.15 | 8.41 | TRUE | 1 | 10.47 |
| ts_m2_b7 | 0.69 | 14.16 | 3.92 | TRUE | 1 | 9.55 |
| ts_m2_b6 | 0.63 | 14.79 | 6.46 | TRUE | 1 | 7.70 |
| ts_m2_b4 | 0.56 | 13.37 | 6.53 | TRUE | 1 | 6.28 |
| ts_m2_b5 | 0.57 | 12.14 | 6.26 | TRUE | 1 | 5.31 |
| ts_m2_b3 | 0.55 | 6.92 | 4.07 | TRUE | 1 | 2.31 |
| ts_m2_b2 | 0.28 | 8.42 | 6.47 | TRUE | 1 | 1.67 |
| ts_m2_b1 | 0.17 | 2.26 | 2.09 | TRUE | 1 | 0.00 |
| ts_m2_b0 | 0.00 | 4.01 | 4.01 | TRUE | 1 | 0.00 |
resources <- get_mon_resources(testlocatie_model2_2verwerkers)
plot(resources, metric = "utilization") +
ggtitle("Resource bezetting") +
ylab("bezetting")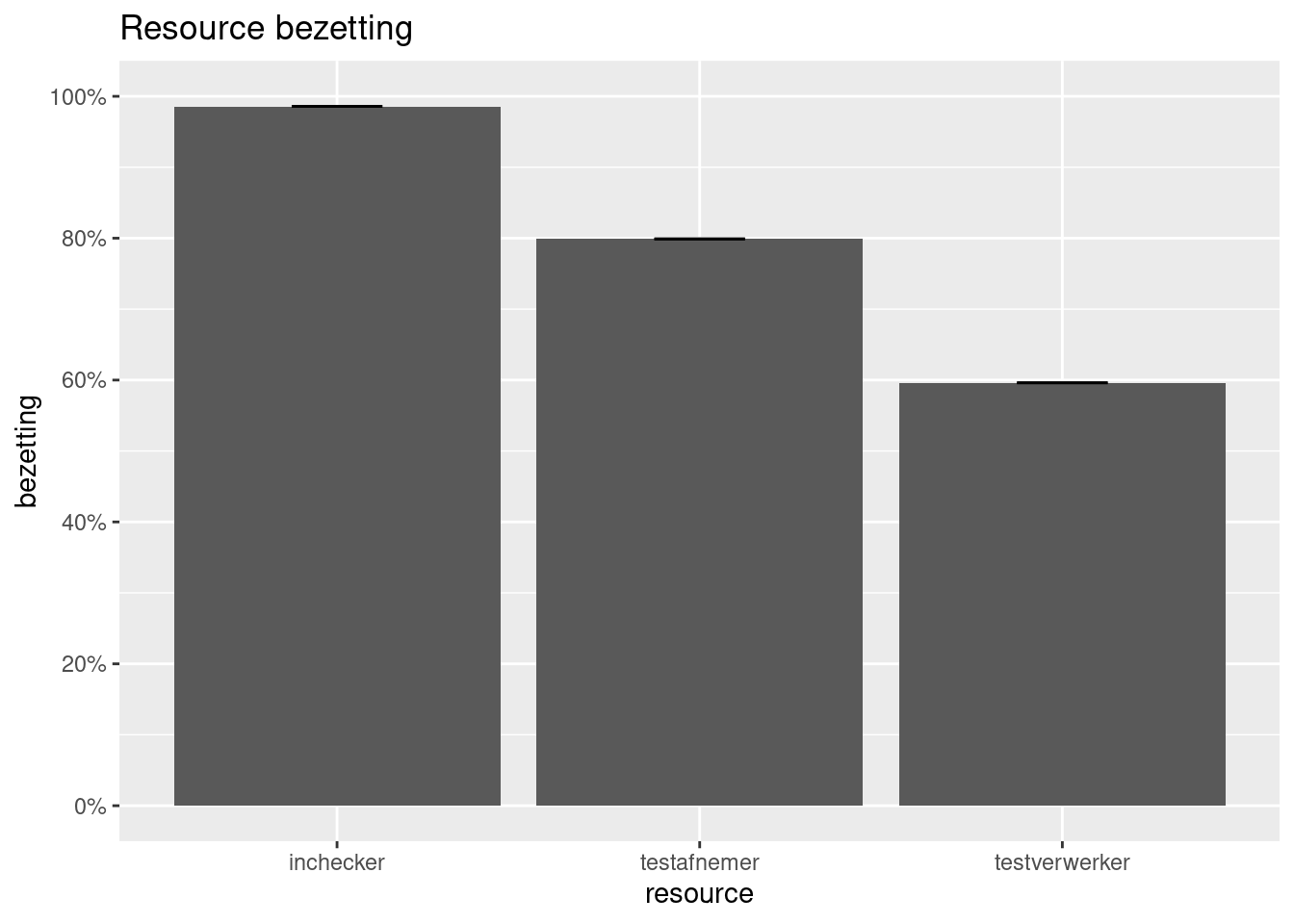
plot(resources, metric = "usage", items = "server") +
labs(title="Resource gebruik") +
xlab("tijd in minuten") +
ylab("in gebruik") 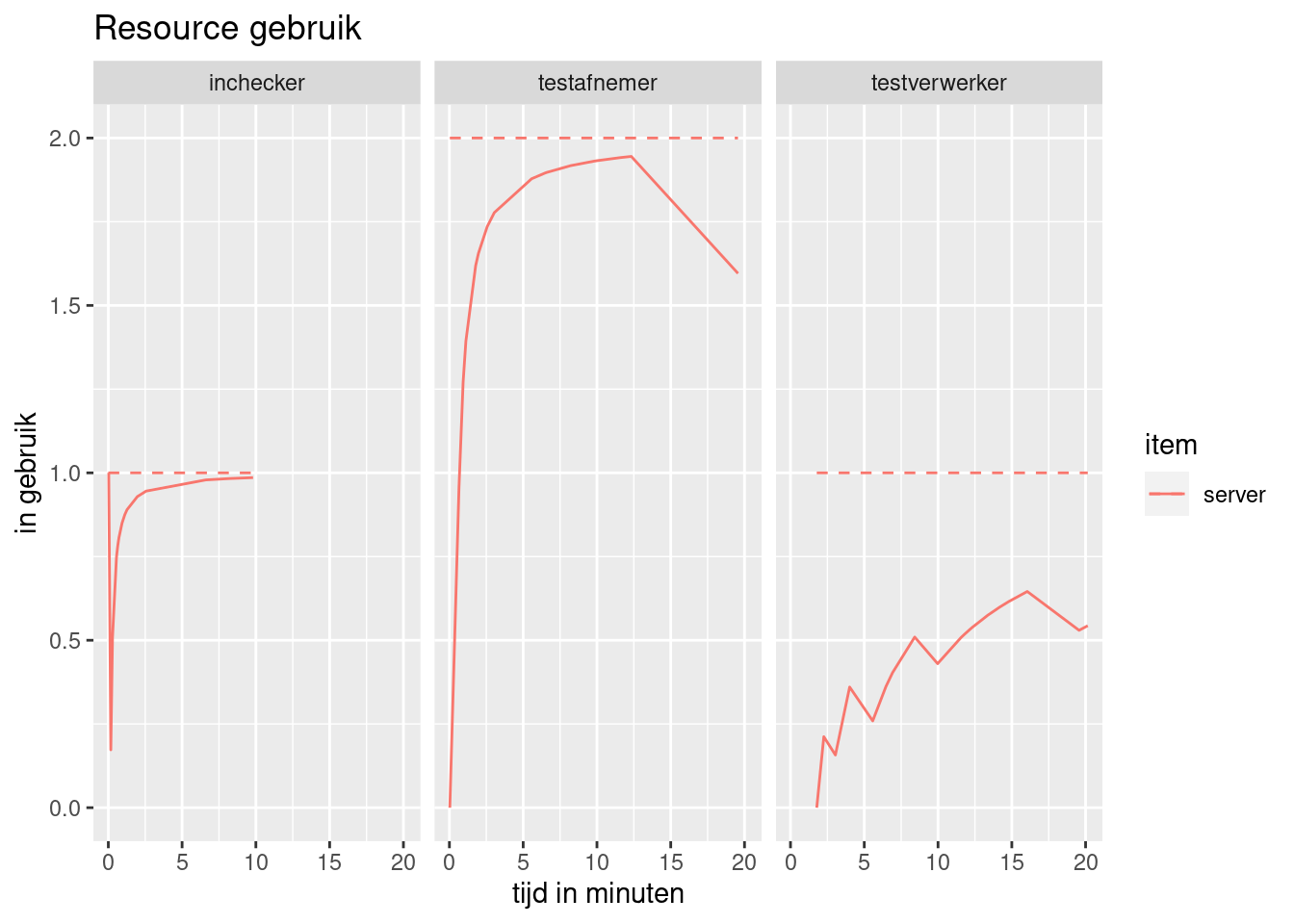
Model 2 met 2 testafnemer-rijen en kortste rij principe
set.seed(123)
teststraat_model2_parallel <- trajectory("Teststraat model2 traject 2") %>%
visit(resource ="inchecker", task = function() rexp(1, 1/inchecktijd)) %>%
select(c("testafnemer1", "testafnemer2"), policy = "shortest-queue") %>%
seize_selected() %>%
timeout(function() {rexp(1, 1/testafneemtijd)}) %>%
release_selected() %>%
visit(resource ="testverwerker",
task = function() rexp(1, 1/testverwerktijd))
testlocatie_model2_parallel <- simmer("teststraatsimulator3") %>%
add_resource("inchecker", 1) %>%
add_resource("testafnemer1", 1) %>%
add_resource("testafnemer2", 1) %>%
add_resource("testverwerker", 1) %>%
add_generator("ts_m2_c", teststraat_model2_parallel,
function() {c(0, rexp(9, clientfrequentie_model2), -1)})testlocatie_model2_parallel %>%
run(until = geopendtijd ) %>%
now()## [1] 36.6776testlocatie_model2_parallel %>%
get_mon_arrivals() %>%
transform(waiting_time =
round(end_time - start_time - activity_time, digits = 2)) %>%
dplyr::arrange(desc(waiting_time)) %>%
knitr::kable("html", digits = 2)| name | start_time | end_time | activity_time | finished | replication | waiting_time |
|---|---|---|---|---|---|---|
| ts_m2_c7 | 17.34 | 30.96 | 3.50 | TRUE | 1 | 10.12 |
| ts_m2_c8 | 18.06 | 31.97 | 7.89 | TRUE | 1 | 6.02 |
| ts_m2_c6 | 15.77 | 29.73 | 8.48 | TRUE | 1 | 5.49 |
| ts_m2_c5 | 14.18 | 25.19 | 6.81 | TRUE | 1 | 4.19 |
| ts_m2_c4 | 13.90 | 22.45 | 8.12 | TRUE | 1 | 0.43 |
| ts_m2_c0 | 0.00 | 3.52 | 3.52 | TRUE | 1 | 0.00 |
| ts_m2_c1 | 4.22 | 5.82 | 1.60 | TRUE | 1 | 0.00 |
| ts_m2_c2 | 7.10 | 13.12 | 6.02 | TRUE | 1 | 0.00 |
| ts_m2_c3 | 13.75 | 17.83 | 4.09 | TRUE | 1 | 0.00 |
| ts_m2_c9 | 31.70 | 36.68 | 4.98 | TRUE | 1 | 0.00 |
resources <- get_mon_resources(testlocatie_model2_parallel)
plot(resources, metric = "utilization", )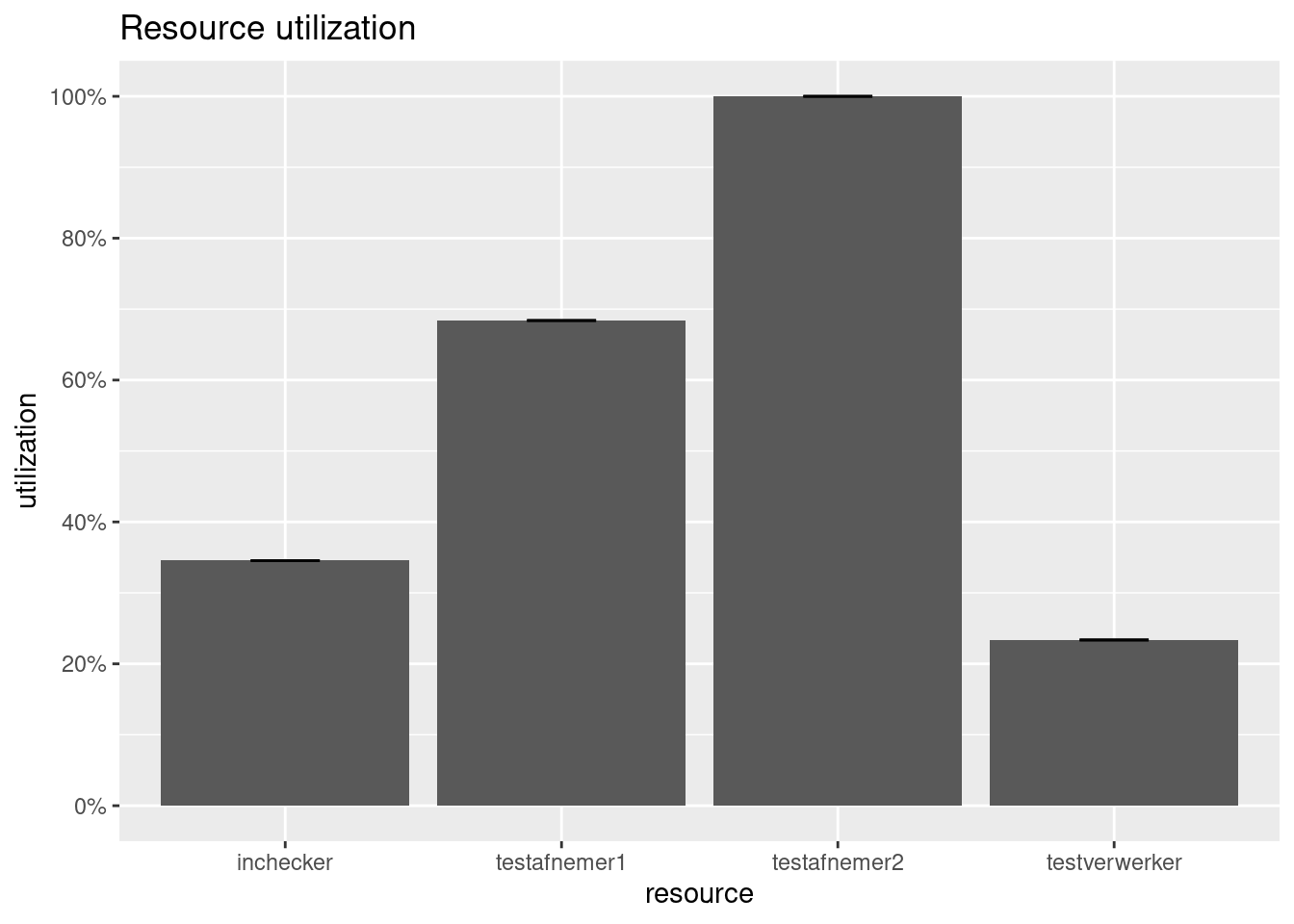
plot(resources, metric = "usage", items = "server") +
labs(title="Resource gebruik") +
xlab("tijd in minuten") +
ylab("in gebruik") 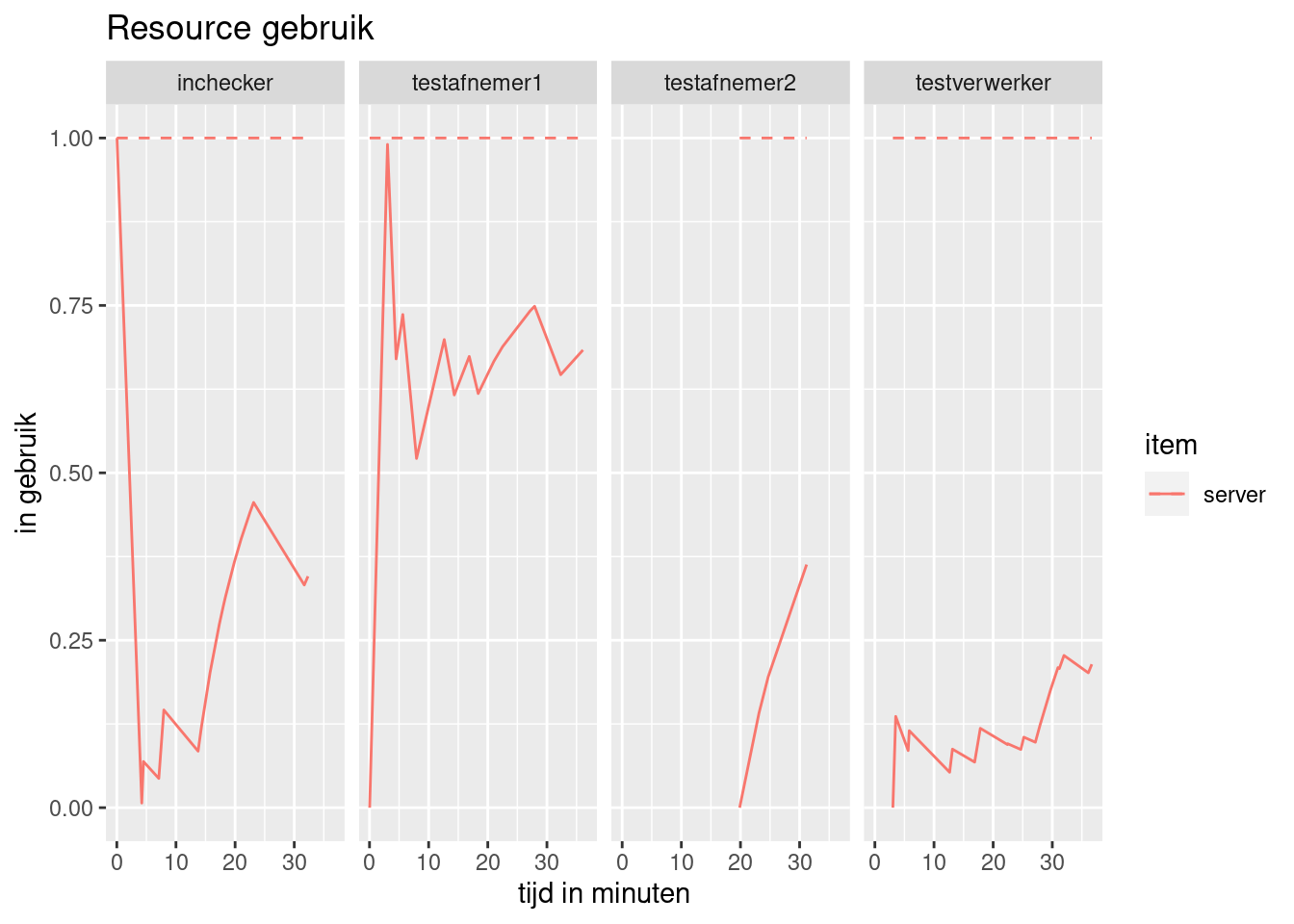
We gaan nu naar wat grotere simulaties van een model 3 testlocatie kijken om een wat betere indruk van het gedrag als geheel te krijgen.
Model 3 testlocatie simulatie
Model 3 is voor een grotere lokatie met o.a. 3 incheckers en testafnemers. We veronderstellen het volgende m.b.t. hoe vaak er een nieuwe client arriveert.
clientfrequentie_model3 <- 1/(5/3) # 3 per 5 minutenOm een beter inzicht in belasting van testlocatie te krijgen simuleren we deze 100 keer, we gebruiken mclapply om de simulatie te paralleliseren. We gaan uit van het splitsen in 3 wachtrijen na het inchecken. Voor keuze van de rij wordt een kortste wachtrij principe gehanteerd. De parameters voor de resources blijven hetzelfde als in model 2. Het traject voor een client kan dan als volgt gedefinieerd worden:
teststraat_model3_traject <- trajectory("Teststraat model 3 traject") %>%
visit(resource ="inchecker", task = function() rexp(1, 1/inchecktijd)) %>%
select(c("testafnemer1", "testafnemer2", "testafnemer3"),
policy = "shortest-queue") %>%
seize_selected() %>%
timeout(function() {rexp(1, 1/testafneemtijd)}) %>%
release_selected() %>%
visit(resource ="testverwerker", task = function() rexp(1, testverwerktijd))Uitgaande van bovenstaande definitie gaan we 100 keer een volledige dag van een testlocatie simuleren.
simulaties_model3 <- mclapply(1:100, function(i) {
simmer("teststraatsimulator4") %>%
add_resource("inchecker", 3) %>%
add_resource("testafnemer1", 1) %>%
add_resource("testafnemer2", 1) %>%
add_resource("testafnemer3", 1) %>%
add_resource("testverwerker", 1) %>%
add_generator("Teststraat model3 traject", teststraat_model3_traject,
function() rexp(1, clientfrequentie_model3)) %>%
run(until = geopendtijd) %>%
wrap()
})Hierna kunnen weer allerlei analyses op de performance gedaan worden. B.v. wat de bezetting van de verschillende soorten medewerkers op de testlocatie is. Daar zien we dat de testafnemer de bottleneck is, logisch want kost het meeste tijd.
resources <- get_mon_resources(simulaties_model3)
plot(resources, metric = "utilization") +
labs(title = "Resource bezetting",
y = "bezetting",
x = "resource")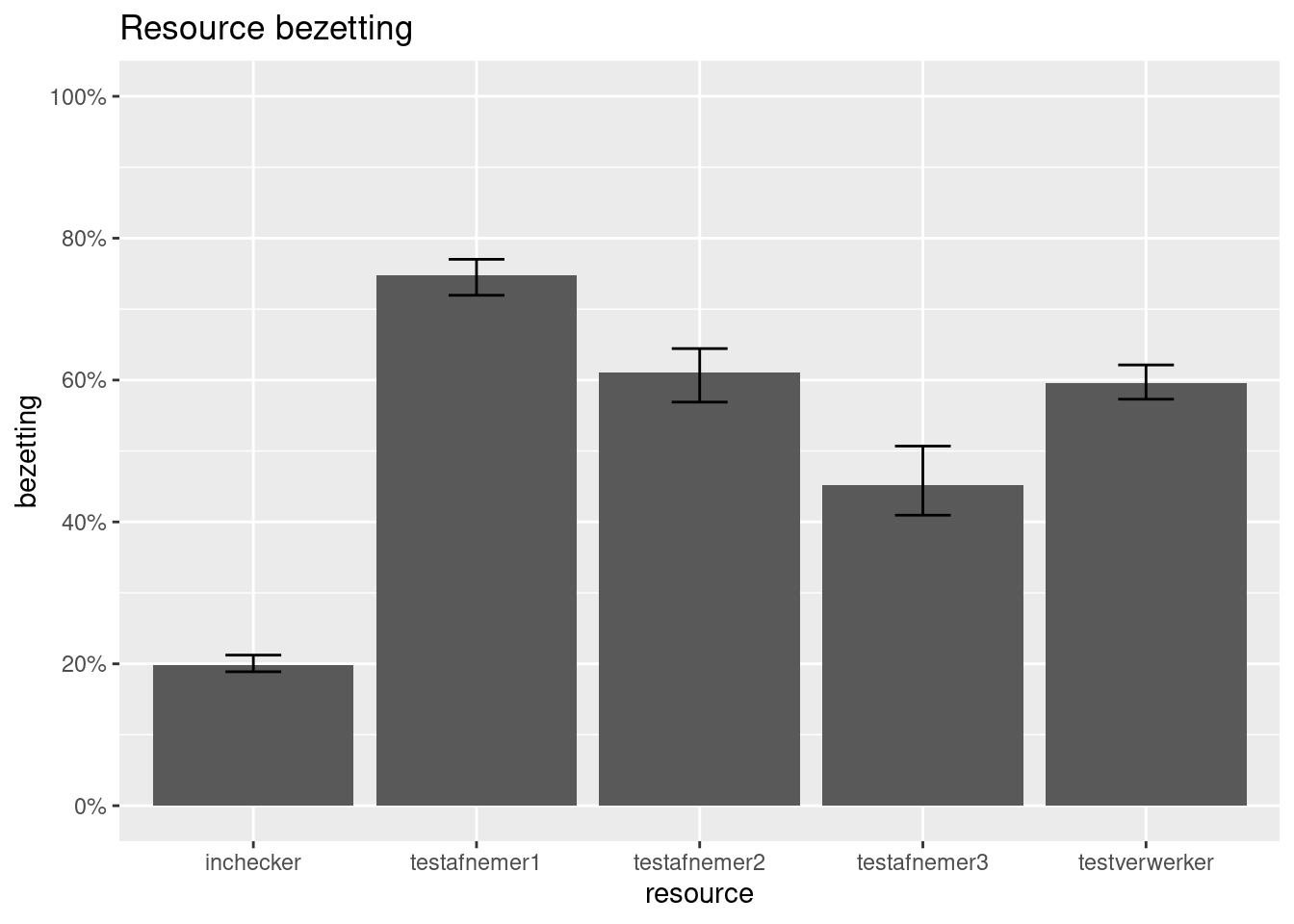
We zien dat de resources goed gebruikt worden, maar nog ruimte hebben voor als er tegenvallers zijn, dat is goed.
plot(resources, metric = "usage", items = "server") +
theme(axis.text.x = element_blank()) +
labs(title = "Resource gebruik",
y = "in gebruik",
x = "simulatietijd in minuten") 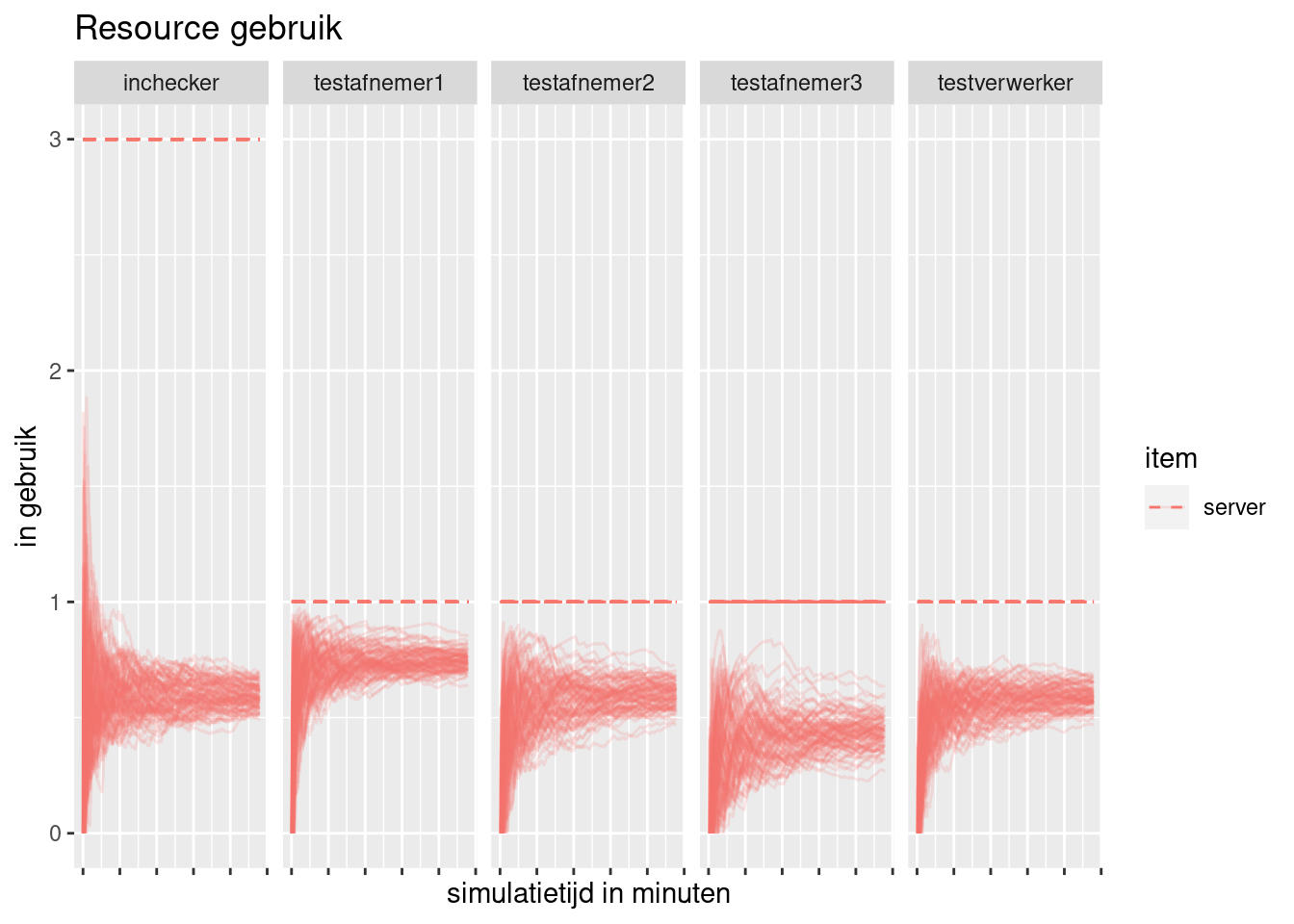
arrivals <- get_mon_arrivals(simulaties_model3)
plot(arrivals, metric = "flow_time") +
geom_smooth(color = "red3") +
ggtitle("Verloop van doorlooptijd in testlocatie") +
ylab("doorlooptijd") +
xlab("simulatietijd in minuten")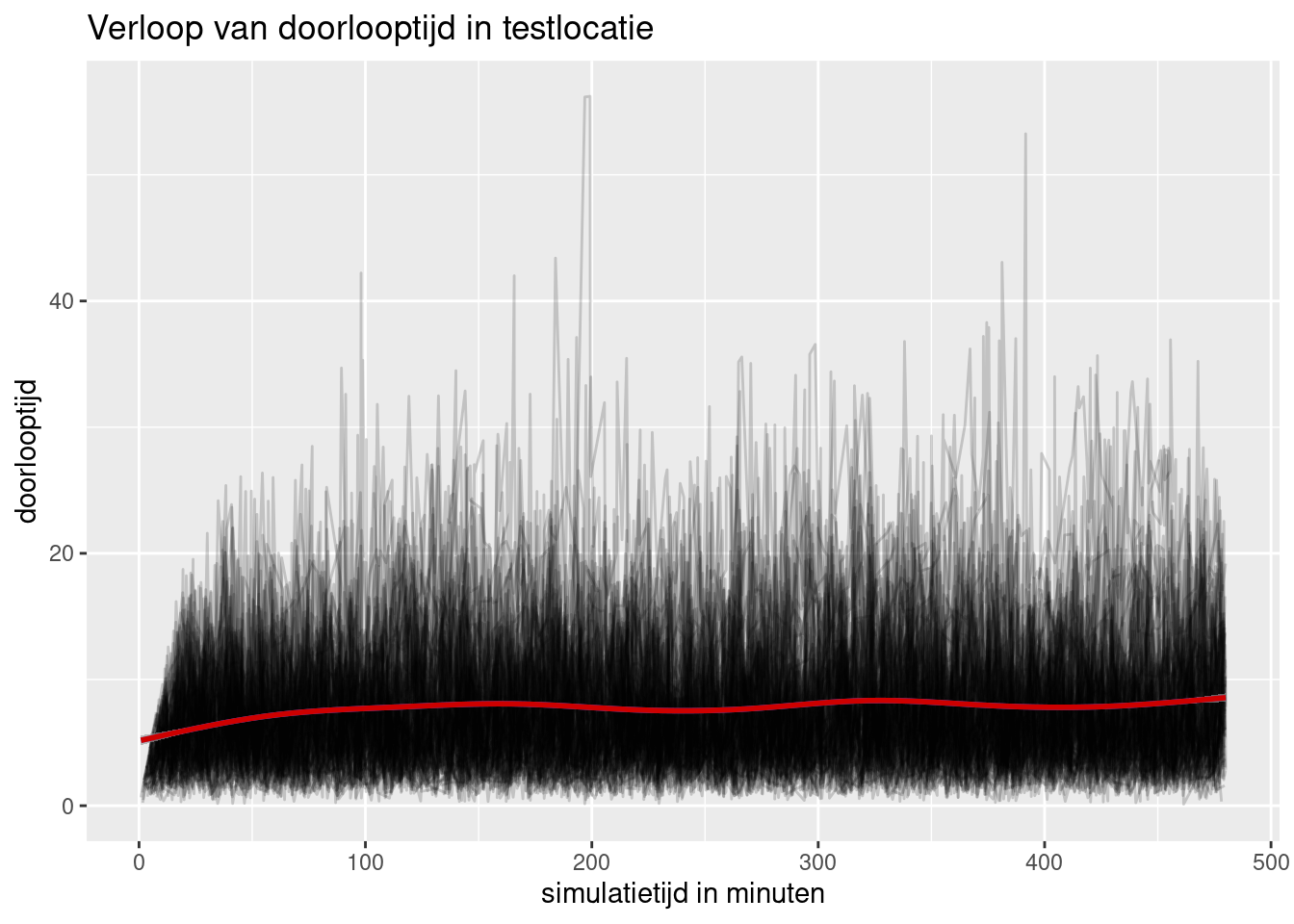
Dit systeem is stabiel gegeven de gekozen parameters. De doorlooptijden lopen niet op. Hieronder nog uitsplitsing in actieve tijd en wachttijd.
plot(arrivals, metric = "activity_time") +
geom_smooth(color = "red3") +
ggtitle("Verloop van de actief bestede tijd") +
ylab("actieve bestede tijd") +
xlab("simulatietijd in minuten")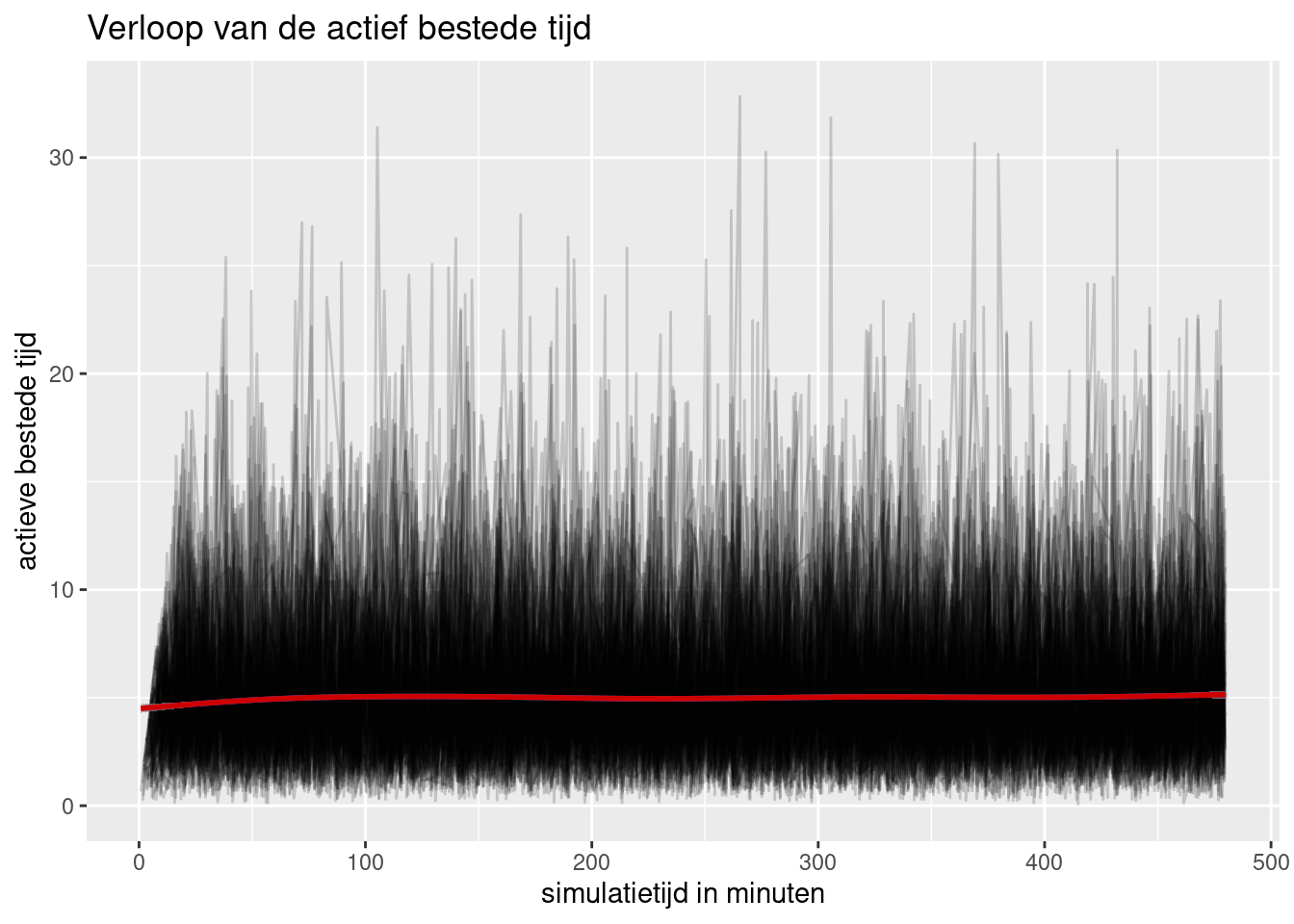
arrivals <- get_mon_arrivals(simulaties_model3)
plot(arrivals, metric = "waiting_time") +
geom_smooth(color = "red3") +
ggtitle("Verloop van de wachtijden") +
ylab("wachttijd") +
xlab("simulatietijd in minuten")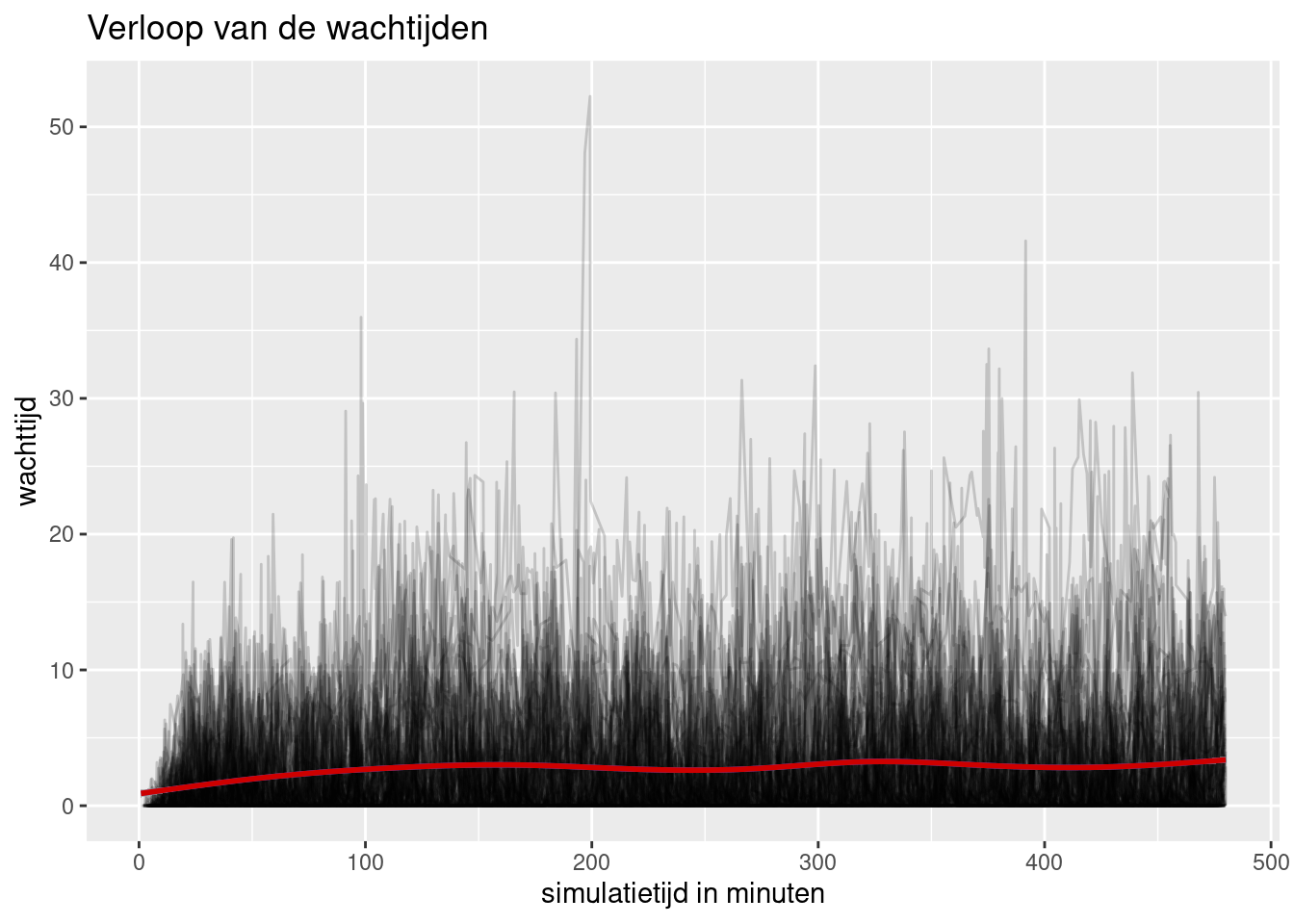
In een volgende post zal ik meer aandacht besteden aan:
- Stresstest testlocatie simuleren, denk o.a. aan praktische eigenschappen van de locatie die beperkingen aan de maximale lengte van wachtrijen.
- Relatie met Kendall’s notatie4 voor wachtrij systemen, bv M/M/1
- Geautomatiseerd visualiseren van het gedefinieerd traject.
Toolkit inrichten testlocatie voor antigeentesten, VNO-NCW, https://werkgeverstesten.prod.websites.vno-ncw.totalservices.io/app/uploads/sites/8/2021/02/20210201_Spoor-2_Toolkit-antigeen-versie-3.1-1.pdf↩︎
Discrete Event Simulation, https://en.wikipedia.org/wiki/Discrete-event_simulation↩︎
simmer R package, https://cloud.r-project.org/package=simmer↩︎
Kendall’s notation, https://en.wikipedia.org/wiki/Kendall%27s_notation↩︎